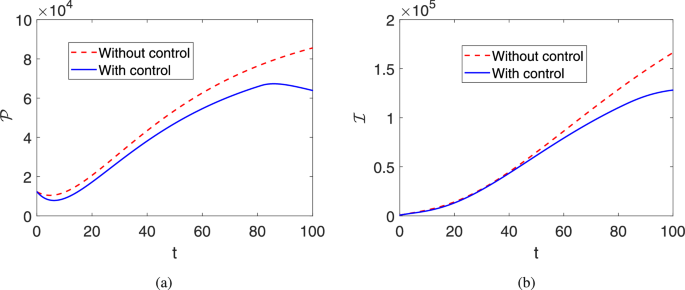
Fractional order breast cancer model with therapy, prevention diagnosis and optimal control based on real data
In this portion, we Analyze the Hyers-Ulam and general Hyers-Ulam stability analysis32,33. Let us suppose \(\epsilon >0\) with, $$\begin{aligned} |^{\textbf{C}}\textbf{D}_{t}^{\alpha _{1}}\mathfrak {S}(t)-\mathfrak {P}(t, \mathfrak {S}(t))|\le \epsilon , ~ t\in \textrm{J}, \end{aligned}$$ (13) for \(\epsilon =\max (\epsilon _{i})^T, i=1,2,3.\) Definition 3.1 Equation (4) is supposed to be Hyers-Ulam stable such that \(\exists , \mathfrak {H}_{\mathfrak {P}}>0,\)